9. Sınıf Meb Matematik Sayfa 161 Cevapları
9. Sınıf Matematik Ders Kitabı Meb Yayınları Sayfa 161 Alıştırmalar Soruları Ve Cevaplarını Yazımızın Devamından Okuyabilirsiniz.
ALIŞTIRMALAR
1. x/y = 3/8 ve y – x = 20 ise x değerini bulunuz.
Çözüm–>>
x/y = 3/8 verilmiş. İçler dışlar çarpımından birbirlerine eşitleyelim.
3x = 8y olur. Yani, 3x-8y = 0
3x-8y = 0
y-x = 20 denklemlerini alt alta toplayalım. İkinci denklemin her elemanını 3 ile çarparsak x’li ifadeler birbirini götürecektir.
3x-8y = 0
3y-3x = 60
-8y+3y = 60
-5y = 60
y = 60/-5
y = -12
y-x denkleminde y’yi yerine yazarsak x’e ulaşırız.
-12-x = 20
-12-20 = x
-32 = x
2. a/b = 3/5 ve b/c = 2 ise a/c değerini bulunuz.
Çözüm–>>
Soruda bize b/c = 2 olarak verilmiş. Bu ifadeden b=2c olarak bulunur. Şimdi bize verilen ilk denklemde b gördüğümüz yere 2c yazarsak a/c değerini bulabiliriz.
a/2c = 3/5 sonucuna ulaştık.
Şimdi a/c’yi elde etmek için eşitliğin her iki tarafını da 2 ile çarparız.
a/c = 6/5
3. (2m + n)/(m-n) = 4 ise m2/n2 değerini bulunuz.
Çözüm–>>
Soruda bize verilen ilk denklemi inceleyerek başlayalım sorumuzu çözmeye.
(2m+n)/(m-n)=4 olarak verilmiş. Biz bu denklemden;
2m+n = 4(m-n) elde edebiliriz.
2m+n = 4m-4n
2m = 5n olarak buluruz.Elimizdeki iki bilinmeyenden kurtulmak için m ve n yerine tek bir değer yazalım.
m = 5k ve n = 2k yazarsak denklemimiz doğru olacaktır.
Şimdi de son olarak m2/n2 yerine değerlerimizi yazalım.
25k2/4k2 bilinmeyen değerler sadeleşir ve geriye yalnızca 25/4 kalır.
4. Bir sınıftaki kız ogrencilerin sayısı 0,24 ile erkek ogrencilerin sayısı 0,36 ile dogru orantılıdır. Sınıf mevcudu 30 dan fazla olduguna gore sınıf mevcudunun en az kac olabilecegini bulunuz.
Çözüm–>>
Sınıftaki kız sayısı 0,24 ile orantılıysa bunu bir k değişkeni ile ifade etmeliyiz. Orantılı olma ifadesi doğru orantılı olmayı ifade ettiğine göre,
Kız öğrenci sayısı= 0,24k
Bu durumda erkek öğrenci sayısı= 0,36k
Öyleyse toplam sınıf mevcudu= 0,24k+0,36k= 0,60k bulunur.
Sınıf mevcudu 30’dan fazla ise eşitsizliğimizi yazalım.
0,60k> 30
k>50 bulunur. Ancak sınıf mevcudu bir tamsayı olabilir ve negatif olamaz. Bu durumda 0,60k= 60k/100 ifadesi ancak 100 ile sadeleşebilecek bir k sayısı olmalıdır. Bu durumda 50’den büyük olan ve 100 ile sadeleşebilecek tek sayı 55 olacaktır. Öyleyse:
(60*55)/100= 33 kişi olabilirler.
5. Akif ve Mert bir arsayı 2/5 oranında hisse ile almak istemektedir. Kucuk hisseyi Akif 32.000 TL karsılıgında aldıgına gore arsanın tamamının kac TL oldugunu bulunuz.
Çözüm–>>
Akif’in hissesine 2k dersek Mert’in hissesi 5k olacaktır. Küçük olan hisse yani Akif’in hissesi 32000 TL olduğuna göre:
2k = 32000 ise k = 16000 TL’dir.
k = 16000 ise 5k = 5 x 16000 = 80000 TL (Akif’in hissesi)
Arsanın tamamı=32000 + 80000 = 112000 TL
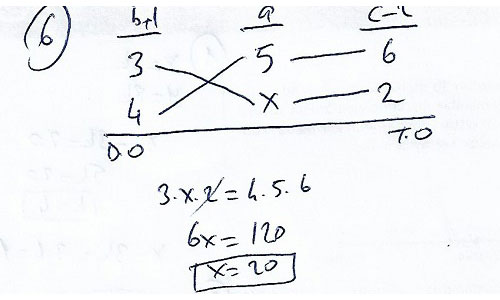
6. a sayısı b+1 ile dogru, c-2 ile ters orantılıdır. a = 5 ve b = 2 iken c = 8 ise b = 3 ve c = 4 iken a degerini bulunuz.
Çözüm–>>
7. Ozdes olan 25 adet gunes panelinin 12 gunde urettigi elektrigi , aynı sartlarda bu panellerle ozdes ve 3 kat daha fazla sayıdaki gunes paneli ile kac gunde uretebilecegini bulunuz.
Çözüm–>>
Bu soru ters orantı kurularak çözülür.Çünkü güneş paneli sayısıyla gün birbirine ters orantılıdır.Güneş paneli sayısı arttıkça daha çok elektrik üretileceği için,aynı miktarda elektrik daha az günde üretilir.
25 adet 12 gün
75 adet x gün
25.12 / 75 =x = 4 günde üretilir.
Aslında buna 75 bile demeden direkt olarak güneş paneli sayısı 3 kat artacaksa gün sayısı da 3 e bölünecek diyebilirdik.
8. Cennet Hanım anaokuluna giden kızı ile hafta sonu kek yapmak istemektedir. Bunun icin gerekli olan un, seker ve tereyagı miktarları sırasıyla 8, 3 ve 2 sayıları ile dogru orantılıdır. Cennet Hanım ve kızının yaptıgı 4 kisilik bir kek 1300 gr olduguna gore yapacakları 8 kisilik bir kekte kac gram tereyagı kullanacaklarını bulunuz.
Çözüm–>>
Soruda verilenlere göre kekin içindeki malzemelerin oranı şu şekildeymiş;
Un : 8 k
Şeker : 3 k
Tereyağı: 2 k
toplamda: 8k + 3k + 2k = 13 k malzeme bulunuyor.
4 kişilik kek 1300 gr ise ⇒ 8 kişilik kek: 1300 gr x 2 = 2600 gr olur.
toplamda malzemeler 13 k olduğuna göre
13 k = 2600 gr
k =200 gr olur.
Tereyağ miktarı 2k ise 200 x 2 = 400 gram tereyağı bulunur.
9. Bir bilim insanı demir, aluminyum ve kursun metallerini sırasıyla 3, 4 ve 12 sayıları ile ters orantılı olacak sekilde karıstırıp 240 gramlık bir alasım elde ediyor. Bu alasımdaki aluminyum miktarını bulunuz.
Çözüm–>>
10. Bir ucak firması bilet fiyatlarını 30 bos koltuk kalana kadar sabit bir fiyatla bos koltuk sayısı 30 un altına dustugunde koltuk sayısı ile ters orantılı olacak sekilde belirlemektedir. 20 bos koltugu olan bir ucakta bilet fiyatı 75 TL ise 15 bos koltuk kaldıgında bilet fiyatının kac TL olacagını bulunuz.
Çözüm–>>
Koltuk sayısı 30’un altına düştüğünde fiyat koltuk sayısı ile ters orantılı olarak belirlendiğine göre:
x/20=75==>x/15=? (soru bu hale geldi)
x=20×75=1500==>x/15=1500/15=100
Bilet fiyatı 100TL olmalı.